lppmunasman.ac.id

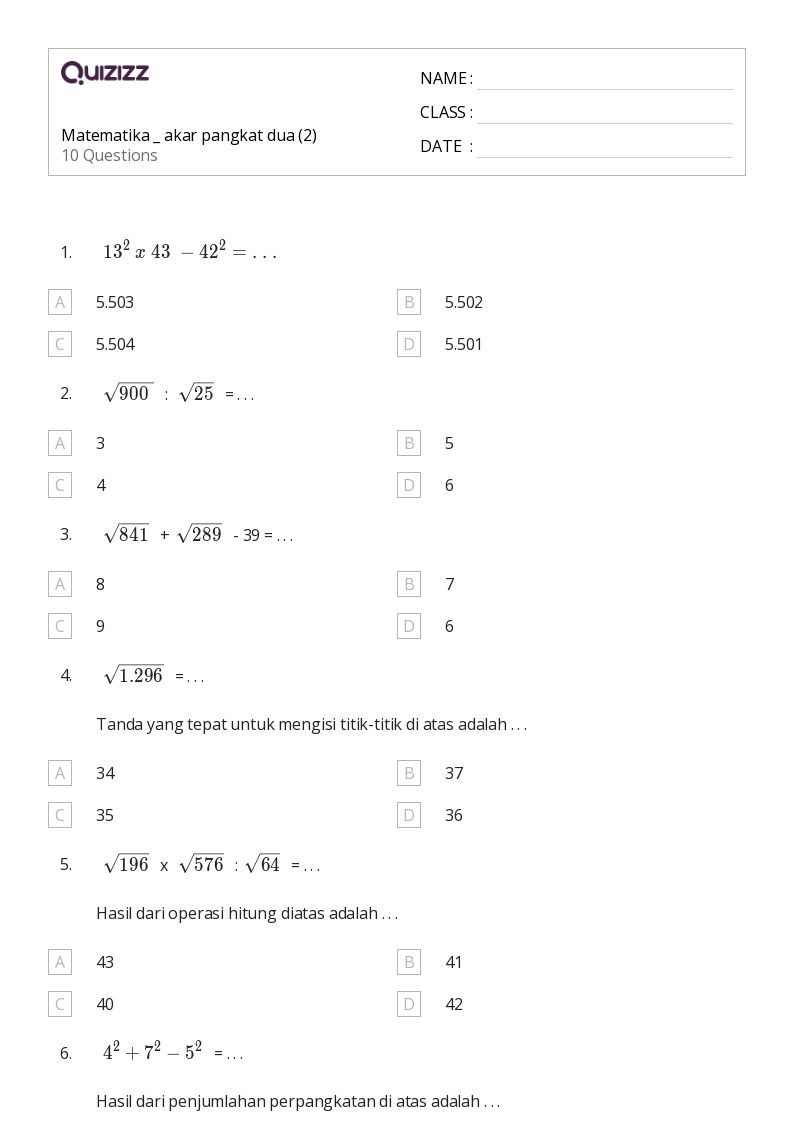
Memahami Akar Pangkat

Halo anak-anak hebat! Hari ini kita akan belajar sesuatu yang baru dan menarik, yaitu tentang akar pangkat. Mungkin kata "akar pangkat" terdengar sedikit rumit, tapi jangan khawatir, kita akan mempelajarinya bersama dengan cara yang menyenangkan dan mudah dipahami.

Apa itu Akar Pangkat?

Sebelum kita melangkah lebih jauh, mari kita pahami dulu apa itu akar pangkat. Akar pangkat adalah kebalikan dari perpangkatan. Ingatkah kalian tentang perpangkatan? Misalnya, 2 pangkat 2 (ditulis 2²) artinya 2 dikalikan 2, hasilnya adalah 4. Nah, akar pangkat adalah kebalikannya. Jika kita punya angka 4, dan kita ingin mencari akar pangkat dua-nya, artinya kita mencari angka berapa yang jika dikalikan dengan dirinya sendiri hasilnya adalah 4. Jawabannya adalah 2. Jadi, akar pangkat dua dari 4 adalah 2.

Dalam matematika, akar pangkat dua biasanya dilambangkan dengan simbol seperti ini: $sqrt$. Jadi, jika kita menulis $sqrt4$, itu artinya kita mencari akar pangkat dua dari 4.

Mengapa Kita Perlu Belajar Akar Pangkat?

Mungkin kalian bertanya-tanya, kenapa kita perlu belajar tentang akar pangkat? Akar pangkat ini sangat berguna lho!

• Menyelesaikan Masalah: Akar pangkat sering muncul dalam berbagai masalah matematika, terutama yang berkaitan dengan bangun datar seperti persegi. Misalnya, jika kita tahu luas sebuah persegi, kita bisa menggunakan akar pangkat untuk mencari panjang sisinya.
• Memahami Konsep Matematika Lain: Memahami akar pangkat akan membantu kalian memahami konsep matematika lain yang lebih kompleks di jenjang selanjutnya.
• Melatih Logika: Belajar akar pangkat juga melatih kemampuan berpikir logis dan analitis kalian.

Akar Pangkat Dua: Teman Kita di Kelas 4 SD

Di kelas 4 SD, kita akan fokus pada akar pangkat dua. Ini adalah jenis akar pangkat yang paling umum kita temui. Ingat, akar pangkat dua dari suatu bilangan adalah bilangan yang jika dikalikan dengan dirinya sendiri menghasilkan bilangan tersebut.

Contohnya:

• $sqrt9$ = ? Angka berapa yang jika dikalikan dengan dirinya sendiri hasilnya 9? Jawabannya adalah 3, karena 3 x 3 = 9. Jadi, $sqrt9 = 3$.
• $sqrt16$ = ? Angka berapa yang jika dikalikan dengan dirinya sendiri hasilnya 16? Jawabannya adalah 4, karena 4 x 4 = 16. Jadi, $sqrt16 = 4$.
• $sqrt25$ = ? Angka berapa yang jika dikalikan dengan dirinya sendiri hasilnya 25? Jawabannya adalah 5, karena 5 x 5 = 25. Jadi, $sqrt25 = 5$.

Mengenal Bilangan Kuadrat Sempurna

Bilangan-bilangan seperti 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, dan seterusnya disebut bilangan kuadrat sempurna. Kenapa disebut bilangan kuadrat sempurna? Karena bilangan-bilangan ini adalah hasil dari perkalian suatu bilangan bulat dengan dirinya sendiri.

• 1 = 1 x 1 (1²)
• 4 = 2 x 2 (2²)
• 9 = 3 x 3 (3²)
• 16 = 4 x 4 (4²)
• 25 = 5 x 5 (5²)
• 36 = 6 x 6 (6²)
• 49 = 7 x 7 (7²)
• 64 = 8 x 8 (8²)
• 81 = 9 x 9 (9²)
• 100 = 10 x 10 (10²)

Dan seterusnya.

Akar pangkat dua dari bilangan kuadrat sempurna adalah bilangan bulat. Misalnya, $sqrt36 = 6$, $sqrt81 = 9$, $sqrt100 = 10$.

Cara Menemukan Akar Pangkat Dua

Ada beberapa cara untuk menemukan akar pangkat dua dari suatu bilangan, terutama bilangan kuadrat sempurna:

1. Mengenali Pola Bilangan Kuadrat: Cara termudah adalah dengan menghafal beberapa bilangan kuadrat sempurna dan akar pangkat duanya. Misalnya, jika kalian melihat angka 49, kalian langsung tahu bahwa akar pangkat duanya adalah 7 karena kalian ingat bahwa 7 x 7 = 49.

2. Mencoba-coba (Trial and Error): Jika kalian tidak yakin, kalian bisa mencoba-coba. Misalnya, kita ingin mencari $sqrt64$. Kita bisa mencoba:

   • 5 x 5 = 25 (terlalu kecil)
   • 6 x 6 = 36 (terlalu kecil)
   • 7 x 7 = 49 (terlalu kecil)
   • 8 x 8 = 64 (pas!)
     Jadi, $sqrt64 = 8$.

3. Menggunakan Faktorisasi Prima (untuk bilangan yang lebih besar): Untuk bilangan yang lebih besar, kita bisa menggunakan metode faktorisasi prima. Namun, untuk kelas 4 SD, fokus utama biasanya adalah mengenali bilangan kuadrat sempurna dan mencoba-coba.

   Contoh dengan faktorisasi prima (ini mungkin sedikit lebih lanjut, tapi bagus untuk diketahui):
   Misalnya mencari $sqrt144$.

   • Faktorisasi prima dari 144:
     144 = 2 x 72
     72 = 2 x 36
     36 = 2 x 18
     18 = 2 x 9
     9 = 3 x 3
     Jadi, 144 = 2 x 2 x 2 x 2 x 3 x 3.
   • Kita kelompokkan faktor yang sama berpasangan: (2 x 2) x (2 x 2) x (3 x 3).
   • Setiap pasangan, kita ambil satu angka: 2 x 2 x 3 = 12.
     Jadi, $sqrt144 = 12$.

Akar Pangkat dan Persegi

Seperti yang disebutkan sebelumnya, akar pangkat dua sangat erat kaitannya dengan bangun datar persegi.

• Luas Persegi: Luas persegi dihitung dengan rumus sisi x sisi, atau sisi².
• Mencari Sisi Persegi: Jika kita tahu luas sebuah persegi, kita bisa mencari panjang sisinya dengan menggunakan akar pangkat dua. Sisi persegi = $sqrttextLuas Persegi$.

Contoh:
Sebuah persegi memiliki luas 36 cm². Berapa panjang sisinya?
Untuk mencari panjang sisinya, kita perlu mencari akar pangkat dua dari 36.
Sisi = $sqrt36$
Kita tahu bahwa 6 x 6 = 36.
Jadi, sisi persegi tersebut adalah 6 cm.

Soal-Soal Latihan Akar Pangkat Kelas 4 SD

Supaya lebih paham, mari kita coba beberapa soal latihan:

1. Hitunglah akar pangkat dua dari bilangan-bilangan berikut:
   a. $sqrt4$
   b. $sqrt49$
   c. $sqrt81$
   d. $sqrt100$
   e. $sqrt64$

2. Tentukan bilangan kuadrat dari angka-angka berikut:
   a. 5²
   b. 7²
   c. 9²
   d. 10²

3. Sebuah persegi memiliki luas 81 m². Berapakah panjang sisi persegi tersebut?

4. Jika 12 x 12 = 144, maka berapakah $sqrt144$?

5. Lengkapi kalimat berikut:
   Akar pangkat dua dari 16 adalah , karena x ____ = 16.

Jawaban Soal Latihan:

1. a. 2, karena 2 x 2 = 4
   b. 7, karena 7 x 7 = 49
   c. 9, karena 9 x 9 = 81
   d. 10, karena 10 x 10 = 100
   e. 8, karena 8 x 8 = 64

2. a. 25 (5 x 5)
   b. 49 (7 x 7)
   c. 81 (9 x 9)
   d. 100 (10 x 10)

3. Sisi persegi = $sqrt81$ = 9 meter.

4. $sqrt144$ = 12.

5. Akar pangkat dua dari 16 adalah 4, karena 4 x 4 = 16.

Kesimpulan

Belajar akar pangkat mungkin terasa baru, tetapi dengan latihan yang cukup, kalian pasti akan menguasainya. Ingatlah bahwa akar pangkat dua adalah kebalikan dari perpangkatan dua. Dengan memahami konsep bilangan kuadrat sempurna dan berlatih soal, kalian akan semakin percaya diri dalam menyelesaikan soal-soal tentang akar pangkat. Terus semangat belajar, anak-anak hebat!