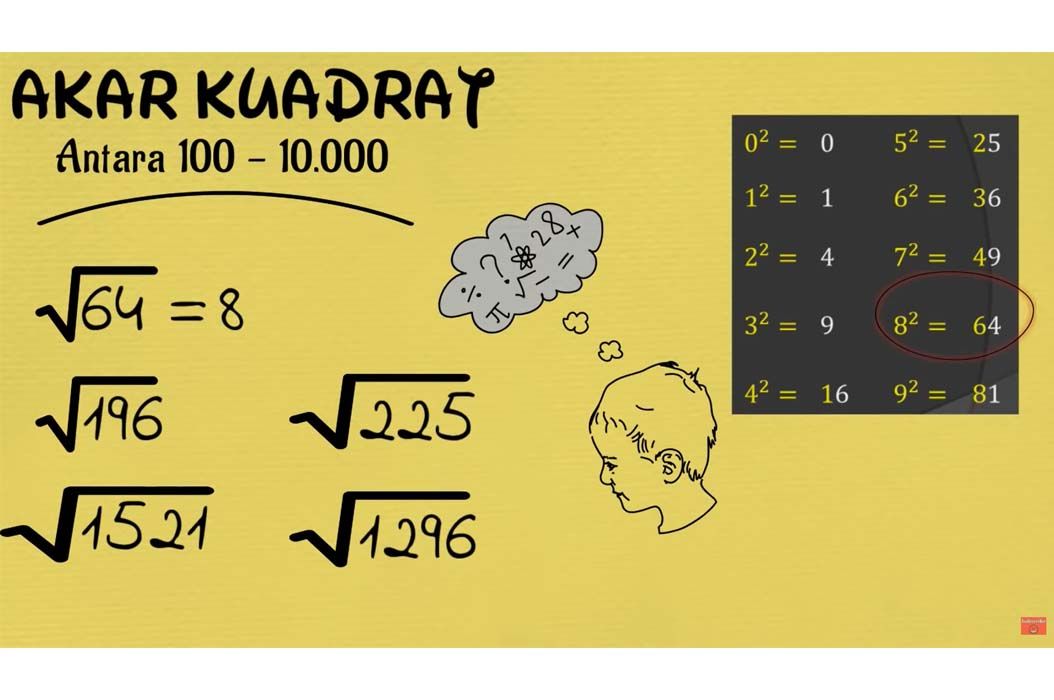
Memahami Akar Pangkat dan Pangkat Dua

Memahami Akar Pangkat dan Pangkat Dua

Halo, para petualang matematika cilik! Hari ini, kita akan menjelajahi dunia angka yang menarik, yaitu tentang pangkat dua dan akar pangkat dua. Mungkin terdengar sedikit rumit pada awalnya, tapi jangan khawatir, kita akan mempelajarinya langkah demi langkah dengan cara yang menyenangkan. Pangkat dua dan akar pangkat dua adalah konsep dasar yang sangat penting dalam matematika. Memahaminya akan membantu kita dalam berbagai perhitungan di masa depan, bahkan dalam kehidupan sehari-hari!

Outline Artikel:

  1. Memahami Akar Pangkat dan Pangkat Dua

    Pendahuluan: Dunia Pangkat dan Akar

    • Apa itu pangkat?
    • Mengapa kita perlu belajar pangkat dua?
    • Pengenalan singkat tentang akar pangkat dua.

  2. Pangkat Dua: Menggandakan Angka

    • Definisi Pangkat Dua (Kuadrat).
    • Notasi Pangkat Dua ($n^2$).
    • Contoh-contoh Sederhana Pangkat Dua.
    • Cara Menghitung Pangkat Dua.
    • Pangkat Dua Angka-angka Penting (1 sampai 10).
    • Pola Menarik pada Pangkat Dua.
    • Aplikasi Pangkat Dua dalam Kehidupan Sehari-hari (Luas Persegi).

  3. Soal-Soal Latihan Pangkat Dua

    • Soal Pilihan Ganda.
    • Soal Isian Singkat.
    • Soal Cerita Sederhana.

  4. Akar Pangkat Dua: Kebalikan Pangkat Dua

    • Apa itu Akar Pangkat Dua?
    • Hubungan Akar Pangkat Dua dengan Pangkat Dua.
    • Notasi Akar Pangkat Dua ($sqrtn$).
    • Mencari Akar Pangkat Dua dari Bilangan Kuadrat Sempurna.
    • Contoh-contoh Sederhana Akar Pangkat Dua.
    • Mencari Akar Pangkat Dua dengan Menggunakan Pengetahuan Pangkat Dua.

  5. Soal-Soal Latihan Akar Pangkat Dua

    • Soal Pilihan Ganda.
    • Soal Isian Singkat.
    • Soal Cerita Sederhana.

  6. Menggabungkan Pangkat Dua dan Akar Pangkat Dua

    • Bagaimana kedua konsep ini saling berhubungan.
    • Contoh soal gabungan.

  7. Penutup: Semangat Belajar Matematika!

    • Rangkuman singkat.
    • Pesan motivasi.

1. Pendahuluan: Dunia Pangkat dan Akar

Bayangkan kita punya sekumpulan permen. Jika kita menggandakan jumlah permen itu, kita akan mendapatkan jumlah yang lebih banyak. Nah, dalam matematika, ada cara khusus untuk menyatakan perkalian berulang seperti ini, yaitu dengan menggunakan "pangkat". Pangkat dua adalah salah satu bentuk pangkat yang paling sering kita jumpai.

Mengapa kita perlu belajar pangkat dua? Pangkat dua seringkali muncul ketika kita menghitung luas sebuah bidang yang bentuknya persegi. Persegi adalah bangun datar yang semua sisinya sama panjang. Jika sisi persegi adalah 5 cm, maka luasnya adalah 5 cm dikalikan 5 cm. Ini adalah contoh sederhana dari pangkat dua.

Lalu, apa itu akar pangkat dua? Akar pangkat dua adalah kebalikan dari pangkat dua. Jika pangkat dua adalah "menggandakan" angka, maka akar pangkat dua adalah mencari angka "asli" yang jika digandakan akan menghasilkan angka tersebut. Seperti mencari asal-usul sebuah angka.

Mari kita mulai petualangan kita!

2. Pangkat Dua: Menggandakan Angka

Definisi Pangkat Dua (Kuadrat)

Pangkat dua dari suatu bilangan adalah hasil perkalian bilangan tersebut dengan dirinya sendiri. Dalam matematika, pangkat dua sering juga disebut "kuadrat".

See also  Mari kita susun artikel tentang soal agama semester ganjil kelas 4, dengan perkiraan panjang 1200 kata, sesuai permintaan Anda.

Notasi Pangkat Dua ($n^2$)

Untuk menyatakan pangkat dua, kita menggunakan angka kecil di atas (disebut eksponen atau pangkat) yang menunjukkan berapa kali bilangan tersebut dikalikan dengan dirinya sendiri. Untuk pangkat dua, eksponennya adalah angka 2.

Contoh:

  • $3^2$ dibaca "tiga pangkat dua" atau "tiga kuadrat".
  • $5^2$ dibaca "lima pangkat dua" atau "lima kuadrat".

Cara Menghitung Pangkat Dua

Untuk menghitung $n^2$, kita cukup mengalikan $n$ dengan $n$.

Contoh:

  • $3^2 = 3 times 3 = 9$
  • $5^2 = 5 times 5 = 25$
  • $10^2 = 10 times 10 = 100$

Pangkat Dua Angka-angka Penting (1 sampai 10)

Menghafal atau memahami pangkat dua dari angka 1 sampai 10 akan sangat membantu kita dalam banyak perhitungan. Mari kita lihat daftarnya:

  • $1^2 = 1 times 1 = 1$
  • $2^2 = 2 times 2 = 4$
  • $3^2 = 3 times 3 = 9$
  • $4^2 = 4 times 4 = 16$
  • $5^2 = 5 times 5 = 25$
  • $6^2 = 6 times 6 = 36$
  • $7^2 = 7 times 7 = 49$
  • $8^2 = 8 times 8 = 64$
  • $9^2 = 9 times 9 = 81$
  • $10^2 = 10 times 10 = 100$

Pola Menarik pada Pangkat Dua

Perhatikan angka terakhir dari hasil pangkat dua:

  • $1^2 = 1$
  • $2^2 = 4$
  • $3^2 = 9$
  • $4^2 = 16$ (angka terakhir 6)
  • $5^2 = 25$ (angka terakhir 5)
  • $6^2 = 36$ (angka terakhir 6)
  • $7^2 = 49$ (angka terakhir 9)
  • $8^2 = 64$ (angka terakhir 4)
  • $9^2 = 81$ (angka terakhir 1)
  • $10^2 = 100$ (angka terakhir 0)

Angka terakhir dari hasil pangkat dua hanya bisa berupa 0, 1, 4, 5, 6, atau 9. Ini adalah pola yang bisa membantu kita mengecek jawaban.

Aplikasi Pangkat Dua dalam Kehidupan Sehari-hari (Luas Persegi)

Pernahkah kamu melihat ubin di lantai atau kertas HVS? Keduanya seringkali berbentuk persegi. Luas sebuah persegi dihitung dengan mengalikan panjang sisinya dengan dirinya sendiri.

Rumus Luas Persegi:
Luas = sisi $times$ sisi
Luas = sisi$^2$

Contoh:
Jika sebuah taman berbentuk persegi memiliki panjang sisi 7 meter, maka luas taman tersebut adalah:
Luas = $7^2$ meter$^2$
Luas = $7 times 7$ meter$^2$
Luas = 49 meter$^2$

3. Soal-Soal Latihan Pangkat Dua

Mari kita uji pemahamanmu dengan beberapa soal latihan!

Soal Pilihan Ganda:

  1. Berapakah hasil dari $4^2$?
    a. 8
    b. 16
    c. 12
    d. 44

  2. Angka berapakah yang jika dipangkatkan dua hasilnya adalah 25?
    a. 4
    b. 5
    c. 6
    d. 10

  3. Luas sebuah persegi dengan panjang sisi 9 cm adalah…
    a. 18 cm$^2$
    b. 27 cm$^2$
    c. 81 cm$^2$
    d. 99 cm$^2$

Soal Isian Singkat:

  1. $6^2$ = ……….
  2. $1^2$ = ……….
  3. Jika sisi sebuah kotak berbentuk persegi adalah 3 meter, maka luasnya adalah ………. meter$^2$.

Soal Cerita Sederhana:

  1. Ibu membeli karpet berbentuk persegi dengan panjang sisi 5 meter. Berapa luas karpet yang dibeli Ibu?

(Jawaban soal latihan akan diberikan di akhir artikel atau bisa didiskusikan secara terpisah agar siswa bisa mencoba terlebih dahulu.)

4. Akar Pangkat Dua: Kebalikan Pangkat Dua

See also  Menguasai Perubahan Kata Massal di Word

Apa itu Akar Pangkat Dua?

Akar pangkat dua adalah operasi matematika yang merupakan kebalikan dari pangkat dua. Jika pangkat dua mengambil sebuah bilangan dan mengalikannya dengan dirinya sendiri untuk mendapatkan hasil, maka akar pangkat dua mengambil sebuah hasil dan mencari bilangan asli yang jika dipangkatkan dua akan menghasilkan angka tersebut.

Hubungan Akar Pangkat Dua dengan Pangkat Dua

Hubungan keduanya sangat erat, seperti teman baik yang selalu berpasangan. Jika kita tahu bahwa $5^2 = 25$, maka kita juga tahu bahwa akar pangkat dua dari 25 adalah 5.

Notasi Akar Pangkat Dua ($sqrtn$)

Simbol yang digunakan untuk akar pangkat dua adalah $sqrt$. Simbol ini disebut "radikal".

Contoh:

  • $sqrt9$ dibaca "akar pangkat dua dari sembilan" atau "akar dari sembilan".
  • $sqrt25$ dibaca "akar pangkat dua dari dua puluh lima" atau "akar dari dua puluh lima".

Mencari Akar Pangkat Dua dari Bilangan Kuadrat Sempurna

Bilangan kuadrat sempurna adalah bilangan yang merupakan hasil dari pangkat dua suatu bilangan bulat (misalnya 1, 4, 9, 16, 25, dan seterusnya). Untuk mencari akar pangkat dua dari bilangan kuadrat sempurna, kita hanya perlu mengingat kembali daftar pangkat dua yang sudah kita pelajari.

Contoh-contoh Sederhana Akar Pangkat Dua

  • Kita tahu bahwa $3^2 = 9$. Maka, $sqrt9 = 3$.
    Ini berarti, angka berapakah yang jika dikalikan dengan dirinya sendiri hasilnya 9? Jawabannya adalah 3.

  • Kita tahu bahwa $4^2 = 16$. Maka, $sqrt16 = 4$.
    Ini berarti, angka berapakah yang jika dikalikan dengan dirinya sendiri hasilnya 16? Jawabannya adalah 4.

  • Kita tahu bahwa $10^2 = 100$. Maka, $sqrt100 = 10$.
    Ini berarti, angka berapakah yang jika dikalikan dengan dirinya sendiri hasilnya 100? Jawabannya adalah 10.

Mencari Akar Pangkat Dua dengan Menggunakan Pengetahuan Pangkat Dua

Cara termudah bagi kita di kelas 4 untuk mencari akar pangkat dua adalah dengan menggunakan ingatan kita tentang pangkat dua.

Misalnya, kita diminta mencari $sqrt36$.
Kita bertanya pada diri sendiri: "Angka berapakah yang jika dikalikan dengan dirinya sendiri hasilnya 36?"
Kita bisa mencoba dari daftar pangkat dua yang kita hafal:

  • $1^2 = 1$
  • $2^2 = 4$
  • $3^2 = 9$
  • $4^2 = 16$
  • $5^2 = 25$
  • $6^2 = 36$
    Aha! Kita menemukan jawabannya. Angka 6 jika dikalikan dengan dirinya sendiri (6 $times$ 6) hasilnya adalah 36.
    Jadi, $sqrt36 = 6$.

5. Soal-Soal Latihan Akar Pangkat Dua

Sekarang, mari kita latih kemampuanmu dalam mencari akar pangkat dua!

Soal Pilihan Ganda:

  1. Berapakah $sqrt49$?
    a. 6
    b. 7
    c. 8
    d. 9

  2. Simbol $sqrt$ disebut juga…
    a. Pangkat dua
    b. Akar pangkat dua
    c. Perkalian
    d. Pembagian

  3. Bilangan berapakah yang jika dipangkatkan dua hasilnya adalah 81?
    a. 7
    b. 8
    c. 9
    d. 10

See also  Latihan Soal Kelas 10 Semester 2

Soal Isian Singkat:

  1. $sqrt64$ = ……….
  2. $sqrt1$ = ……….
  3. Jika luas sebuah meja berbentuk persegi adalah 16 dm$^2$, maka panjang sisinya adalah ………. dm.

Soal Cerita Sederhana:

  1. Seorang petani memiliki sebidang tanah berbentuk persegi. Jika luas tanahnya adalah 49 meter persegi, berapakah panjang sisi tanah petani tersebut?

6. Menggabungkan Pangkat Dua dan Akar Pangkat Dua

Sekarang kita sudah mengenal kedua konsep ini. Mari kita lihat bagaimana mereka bekerja sama. Pangkat dua dan akar pangkat dua adalah operasi yang saling membatalkan.

  • Jika kita punya angka, lalu kita pangkatkan dua, dan kemudian kita ambil akar pangkat duanya, kita akan kembali ke angka semula.
    Contoh:
    Mulai dengan angka 5.
    Pangkatkan dua: $5^2 = 25$.
    Ambil akar pangkat duanya: $sqrt25 = 5$.
    Kita kembali ke angka 5.

  • Sebaliknya, jika kita punya angka, lalu kita ambil akar pangkat duanya, dan kemudian kita pangkatkan dua hasilnya, kita akan kembali ke angka semula.
    Contoh:
    Mulai dengan angka 36.
    Ambil akar pangkat duanya: $sqrt36 = 6$.
    Pangkatkan dua hasilnya: $6^2 = 36$.
    Kita kembali ke angka 36.

Contoh Soal Gabungan:

  1. Hitunglah: $(sqrt81)^2$

    • Pertama, cari $sqrt81$. Kita tahu $9^2 = 81$, jadi $sqrt81 = 9$.
    • Kemudian, pangkatkan dua hasilnya: $9^2 = 81$.
    • Jadi, $(sqrt81)^2 = 81$.

  2. Hitunglah: $sqrt7^2$

    • Pertama, hitung $7^2$. Kita tahu $7^2 = 49$.
    • Kemudian, cari akar pangkat dua dari hasilnya: $sqrt49$. Kita tahu $7^2 = 49$, jadi $sqrt49 = 7$.
    • Jadi, $sqrt7^2 = 7$.

Soal-soal seperti ini menunjukkan betapa kuatnya hubungan timbal balik antara pangkat dua dan akar pangkat dua.

7. Penutup: Semangat Belajar Matematika!

Hebat! Kalian telah menyelesaikan petualangan belajar tentang pangkat dua dan akar pangkat dua. Kita sudah belajar apa itu pangkat dua, cara menghitungnya, dan bagaimana ia digunakan untuk menghitung luas persegi. Kita juga sudah belajar tentang akar pangkat dua sebagai kebalikan dari pangkat dua, dan cara mencarinya dengan mengingat tabel pangkat dua.

Ingatlah, matematika itu seperti permainan. Semakin sering kita berlatih, semakin mahir kita jadinya. Jangan takut untuk mencoba soal-soal baru dan bertanya jika ada yang tidak dimengerti. Teruslah berlatih, dan kalian akan menjadi ahli matematika yang hebat!

Jawaban Soal Latihan:

Pangkat Dua:

  1. b. 16
  2. b. 5
  3. c. 81 cm$^2$
  4. 36
  5. 1
  6. 9 meter$^2$
  7. Luas = $5^2$ meter$^2$ = 25 meter$^2$. Ibu membeli karpet seluas 25 meter persegi.

Akar Pangkat Dua:

  1. b. 7
  2. b. Akar pangkat dua
  3. c. 9
  4. 8
  5. 1
  6. 4 dm
  7. Panjang sisi = $sqrt49$ meter = 7 meter. Panjang sisi tanah petani tersebut adalah 7 meter.